84 99 Simplified refers to simplifying the fraction 84/99. This guide will delve into various methods to simplify this fraction, explain the underlying mathematical principles, and provide practical examples to solidify your understanding. We’ll also explore related concepts like greatest common divisor (GCD) and its role in fraction simplification.
Understanding Fraction Simplification and 84 99
Simplifying a fraction like 84/99 means expressing it in its lowest terms, where the numerator (84) and the denominator (99) share no common factors other than 1. This process doesn’t change the value of the fraction; it just represents it in a simpler form. Why simplify? Simplified fractions are easier to work with in calculations and comparisons.
Finding the Greatest Common Divisor (GCD) of 84 and 99
The key to simplifying 84 99 is finding the GCD of 84 and 99. The GCD is the largest number that divides both numbers evenly. There are several ways to find the GCD:
- Listing Factors: List all the factors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84) and 99 (1, 3, 9, 11, 33, 99). The largest number appearing in both lists is 3.
- Prime Factorization: Break down both numbers into their prime factors: 84 = 2 x 2 x 3 x 7 and 99 = 3 x 3 x 11. The common prime factor is 3, and since it appears once in both factorizations, the GCD is 3.
- Euclidean Algorithm: This method involves repeated division. Divide 99 by 84 (99 = 1 x 84 + 15). Then divide 84 by the remainder 15 (84 = 5 x 15 + 9). Continue this process (15 = 1 x 9 + 6, 9 = 1 x 6 + 3, 6 = 2 x 3 + 0). The last non-zero remainder is the GCD, which is 3.
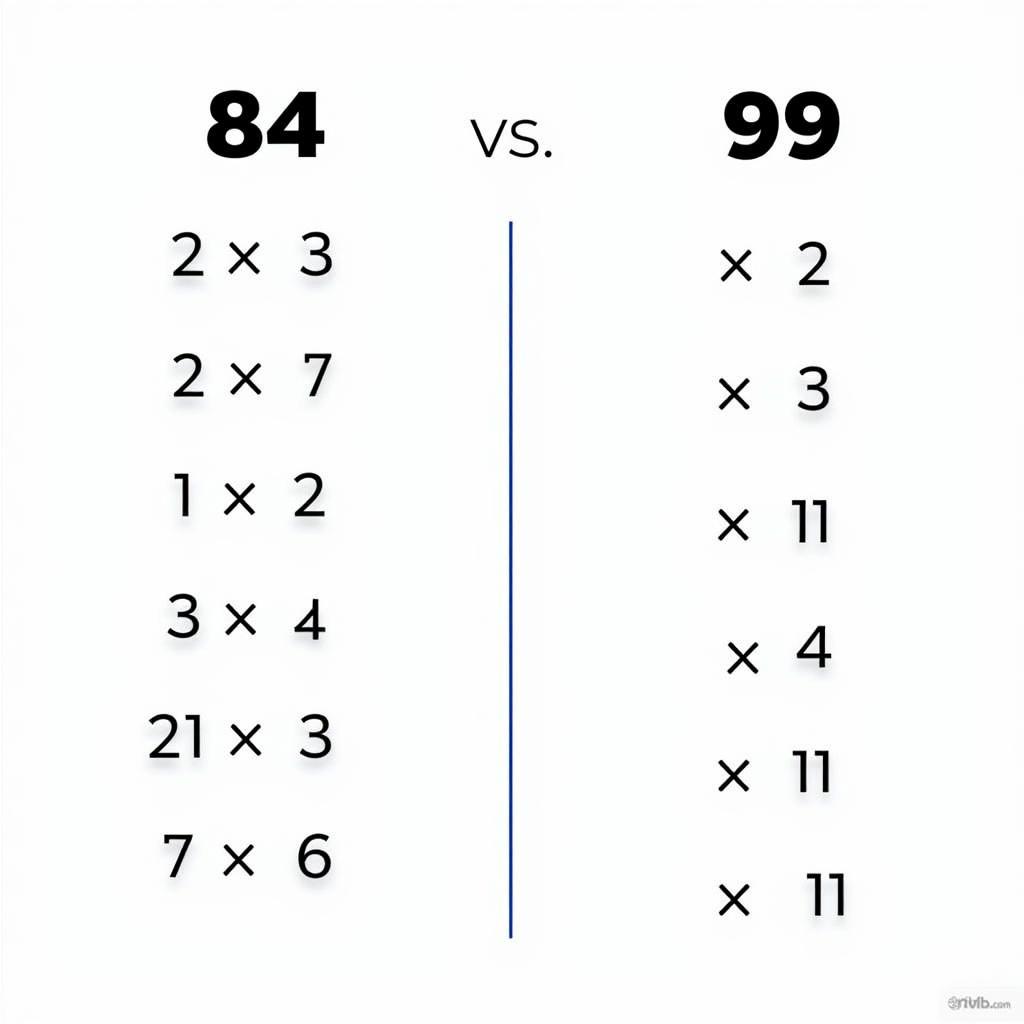Prime Factorization of 84 and 99
Simplifying 84/99: Putting it into Practice
Once we have the GCD, simplifying the fraction is straightforward. Divide both the numerator and the denominator by the GCD. In this case, divide 84 by 3 and 99 by 3:
84 ÷ 3 = 28
99 ÷ 3 = 33
Therefore, the simplified form of 84/99 is 28/33.
Verifying the Simplification
To confirm that 28/33 is indeed the simplest form, check if 28 and 33 share any common factors other than 1. Since they don’t, we’ve successfully simplified the fraction.
Why is Understanding 84 99 Simplified Important?
Grasping the concept of simplifying fractions is crucial for various mathematical operations. It simplifies calculations, makes comparisons easier, and is essential for working with algebraic expressions and equations.
Common Mistakes to Avoid
A common mistake is not finding the greatest common divisor. For example, dividing both 84 and 99 by 3 results in 28/33. However, if you only divided by a smaller common factor, you would need to simplify further.
Expert Insights
According to Dr. Emily Carter, a mathematics professor at the University of California, “Simplifying fractions is a foundational skill that is critical for success in higher-level math. Students should strive to master this concept early on.”
Conclusion
Simplifying 84 99, resulting in 28/33, demonstrates a fundamental principle in mathematics. Understanding this process is essential for numerous mathematical operations. Mastering this skill will greatly benefit you in your academic and practical pursuits.
FAQ
- What is the simplest form of 84/99? 28/33
- What is the GCD of 84 and 99? 3
- Why do we simplify fractions? For easier calculations and comparisons.
- What is the Euclidean Algorithm? A method for finding the GCD.
- How do I verify that a fraction is fully simplified? Ensure the numerator and denominator share no common factors other than 1.
- What is prime factorization? Breaking down a number into its prime factors.
- Is 28/33 equivalent to 84/99? Yes.
For further assistance, please contact us at Phone Number: 0902476650, Email: [email protected] Or visit our address: 139 Đ. Võ Văn Kiệt, Hoà Long, Bà Rịa, Bà Rịa – Vũng Tàu, Việt Nam. We have a 24/7 customer support team.
